Création de tableaux

Complément - niveau basique¶

Passons rapidement en revue quelques méthodes pour créer des tableaux numpy.

import numpy as np

Non initialisé : np.empty¶

La méthode la plus efficace pour créer un tableau numpy consiste à faire l’allocation de la mémoire mais sans l’initialiser :

memory = np.empty(dtype=np.int8,
                  shape=(1_000, 1_000))

J’en profite pour attirer votre attention sur l’impression des gros tableaux où l’on s’efforce de vous montrer les coins :

print(memory)

[[0 0 0 ... 0 0 0]
 [0 0 0 ... 0 0 0]
 [0 0 0 ... 0 0 0]
 ...
 [0 0 0 ... 0 0 0]
 [0 0 0 ... 0 0 0]
 [0 0 0 ... 0 0 0]]

Il se peut que vous voyiez ici des valeurs particulières ; selon votre OS, il y a une probabilité non nulle que vous ne voyiez ici que des zéros. C’est un peu comme avec les dictionnaires qui, depuis la version 3.6, peuvent donner l’impression de conserver l’ordre dans lequel les clés ont été créées. Ici c’est un peu la même chose, vous ne devez pas écrire un programme qui repose sur le fait que np.empty retourne un tableau garni de zéros (utilisez alors np.zeros, que l’on va voir tout de suite).

Tableaux constants¶

On peut aussi créer et initialiser un tableau avec np.zeros et np.ones :

zeros = np.zeros(dtype=np.complex128, shape=(1_000, 100))
print(zeros)

[[0.+0.j 0.+0.j 0.+0.j ... 0.+0.j 0.+0.j 0.+0.j]
 [0.+0.j 0.+0.j 0.+0.j ... 0.+0.j 0.+0.j 0.+0.j]
 [0.+0.j 0.+0.j 0.+0.j ... 0.+0.j 0.+0.j 0.+0.j]
 ...
 [0.+0.j 0.+0.j 0.+0.j ... 0.+0.j 0.+0.j 0.+0.j]
 [0.+0.j 0.+0.j 0.+0.j ... 0.+0.j 0.+0.j 0.+0.j]
 [0.+0.j 0.+0.j 0.+0.j ... 0.+0.j 0.+0.j 0.+0.j]]

fours = 4 * np.ones(dtype=float, shape=(8, 8))
fours

Progression arithmétique : arange¶

En guise de rappel, avec arange on peut créer des tableaux de valeurs espacées d’une valeur constante. Ça ressemble donc un peu au range de Python natif :

np.arange(4)

np.arange(1, 5)

Sauf qu’on peut y passer un pas qui n’est pas entier :

np.arange(5, 7, .5)

Progression arithmétique : linspace¶

Mais bien souvent, plutôt que de préciser le pas entre deux valeurs, on préfère préciser le nombre de points ; et aussi inclure la deuxième borne. C’est ce que fait linspace, c’est très utile pour modéliser une fonction sur un intervalle ; on a déjà vu des exemples de ce genre :

%matplotlib inline
import matplotlib.pyplot as plt
plt.ion()

X = np.linspace(-3., +3.)
Y = np.exp(X)

plt.plot(X, Y);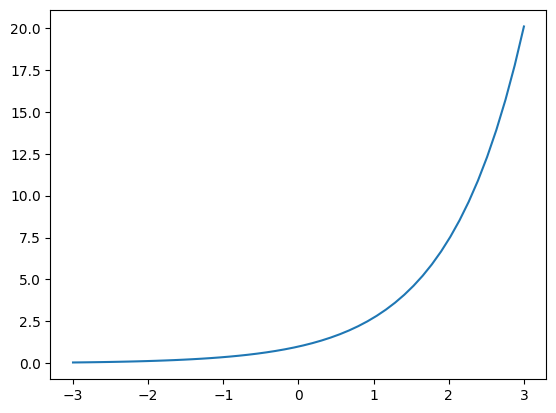

# par défaut linspace crée 50 points
# avec moins de points

X = np.linspace(1/10, 10, num = 5)
plt.plot(X, np.log(X));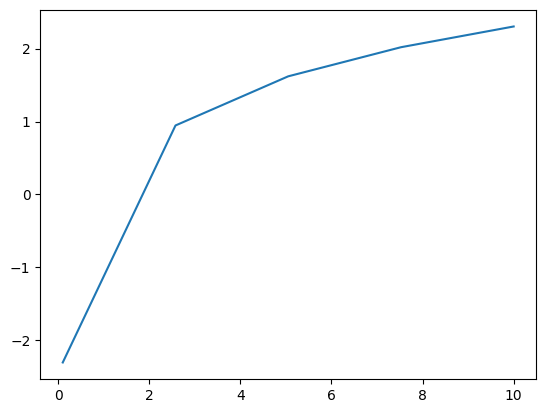

Pour des intervalles en progression géométrique, voyez np.geomspace.

Multi-dimensions : indices¶

La méthode np.indices se comporte un peu comme arange mais pour plusieurs directions ; voyons ça sur un exemple :

ix, iy = np.indices((3, 5))

ix

iy

Cette fonction s’appelle indices parce qu’elle produit des tableaux (ici 2 car on lui a passé une shape à deux dimensions) qui contiennent, à la case (i, j), $i$ (pour le premier tableau) ou $j$ pour le second.

Ainsi, si vous voulez construire un tableau de taille (2, 4) dans lequel, par exemple :

tab[i, j] = 200*i + 2*j + 50

Vous n’avez qu’à faire :

ix, iy = np.indices((2, 4))
tab = 200*ix + 2*iy + 50
tab

Multi-dimensions : meshgrid¶

Si vous voulez créer un tableau un peu comme avec linspace, mais en plusieurs dimensions : imaginez par exemple que vous voulez tracer une fonction à deux entrées :

$f : (x, y) \longrightarrow cos(x) + cos^2(y)$

Sur un pavé délimité par :

$x \in [-\pi, +\pi], y \in [3\pi, 5\pi]$

Il vous faut donc créer un tableau, disons de 50 x 50 points, qui réalise un maillage uniforme de ce pavé, et pour ça vous pouvez utiliser meshgrid. Pour commencer :

# on fabrique deux tableaux qui échantillonnent
# de manière uniforme les intervalles en X et en Y
# on prend un pas de 10 dans les deux sens, ça nous donnera
# 100 points pour couvrir l'espace carré qui nous intéresse

Xticks, Yticks = (np.linspace(-np.pi, np.pi, num=10),
                  np.linspace(3*np.pi, 5*np.pi, num=10))

Avec meshgrid, on va créer deux tableaux, qui sont respectivement les (100) X et les (100) Y de notre maillage :

# avec meshgrid on les croise
# ça fait comme un produit cartésien, 
# en extrayant les X et les Y du résultat

X, Y = np.meshgrid(Xticks, Yticks)

# chacun des deux est donc de taille 10 x 10
X.shape, Y.shape

Que peut-on faire avec ça ? Eh bien, en fait, on a tout ce qu’il nous faut pour afficher notre fonction :

# un tableau 10 x 10 qui contient les images de f()
# sur les points de la grille
Z = np.cos(X) + np.cos(Y)**2

from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_wireframe(X, Y, Z);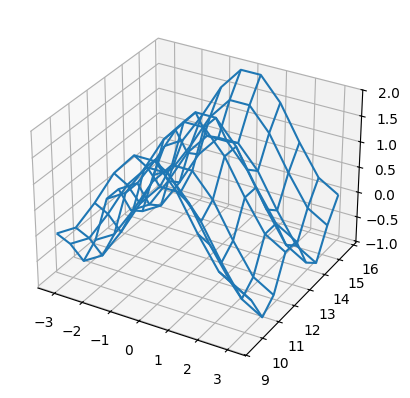

Je vous laisse vous convaincre qu’il est facile d’écrire np.indices à partir de np.meshgrid et np.arange.