numpy en dimension 1

Complément - niveau basique¶

Comme on l’a vu dans la vidéo, numpy est une bibliothèque qui offre un type supplémentaire par rapport aux types de base Python : le tableau, qui s’appelle en anglais array (en fait techniquement, ndarray, pour n-dimension array).

Bien que techniquement ce type ne fasse pas partie des types de base de Python, il est extrêmement puissant, et surtout beaucoup plus efficace que les types de base, dès lors qu’on manipule des données qui ont la bonne forme, ce qui est le cas dans un grand nombre de domaines.

Aussi, si vous utilisez une bibliothèque de calcul scientifique, la quasi totalité des objets que vous serez amenés à manipuler seront des tableaux numpy.

Dans cette première partie nous allons commencer avec des tableaux à une dimension, et voir comment les créer et les manipuler.

import numpy as np

The history saving thread hit an unexpected error (OperationalError('disk I/O error')).History will not be written to the database.

Création à partir de données¶

np.array¶

On peut créer un tableau numpy à partir d’une liste - ou plus généralement un itérable - avec la fonction np.array comme ceci :

array = np.array([12, 25, 32, 55])
array

Attention : une erreur commune au début consiste à faire ceci, qui ne marche pas :

try:
    array = np.array(1, 2, 3, 4)
except Exception as e:
    print(f"OOPS, {type(e)}, {e}")

OOPS, <class 'TypeError'>, array() takes from 1 to 2 positional arguments but 4 were given

Ça marche aussi à partir d’un itérable :

builtin_range = np.array(range(10))
builtin_range

Création d’intervalles¶

np.arange¶

Sauf que dans ce cas précis on préfèrera utiliser directement la méthode arange de numpy :

numpy_range = np.arange(10)
numpy_range

Avec l’avantage qu’avec cette méthode on peut donner des bornes et un pas d’incrément qui ne sont pas entiers :

numpy_range_f = np.arange(1.0, 2.0, 0.1)
numpy_range_f

np.linspace¶

Aussi et surtout, lorsqu’on veut créer un intervalle dont on connaît les bornes, il est souvent plus facile d’utiliser linspace, qui crée un intervalle un peu comme arange, mais on lui précise un nombre de points plutôt qu’un pas :

X = np.linspace(0., 10., 50)
X

Vous remarquez que les 50 points couvrent à intervalles réguliers l’espace compris entre 0 et 10 inclusivement. Notons que 50 est aussi le nombre de points par défaut. Cette fonction est très utilisée lorsqu’on veut dessiner une fonction entre deux bornes, on a déjà eu l’occasion de le faire :

import matplotlib.pyplot as plt
%matplotlib inline
plt.ion()

# il est d'usage d'ajouter un point-virgule à la fin de la dernière ligne
# si on ne le fait pas (essayez..), on obtient l'affichage d'une ligne
# de bruit qui n'apporte rien
Y = np.cos(X)
plt.plot(X, Y);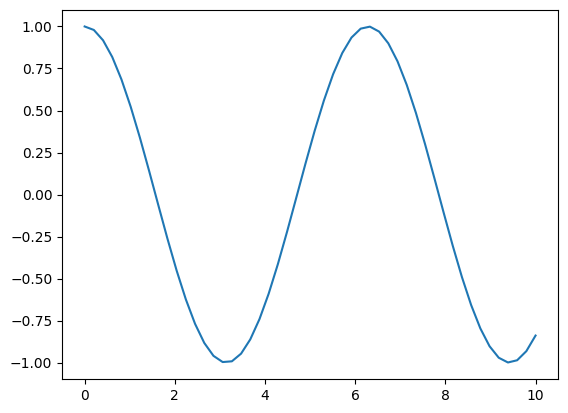

Programmation vectorielle¶

Attardons-nous un petit peu :

• nous avons créé un tableau X de 50 points qui couvrent l’intervalle $[0..10]$ de manière uniforme,

• et nous avons calculé un tableau Y de 50 valeurs qui correspondent aux cosinus des valeurs de X.

Remarquez qu’on a fait ce premier calcul sans même savoir comment accéder aux éléments d’un tableau. Vous vous doutez bien qu’on va accèder aux éléments d’un tableau à base d’index, on le verra bien sûr, mais on n’en a pas eu besoin ici.

En fait en numpy on passe son temps à écrire des expressions dont les éléments sont des tableaux, et cela produit des opérations membre à membre, comme on vient de le voir avec cosinus.

Ainsi pour tracer la fonction $x \longrightarrow cos^2(x) + sin^2(x) + 3$ on fera tout simplement :

# l'énorme majorité du temps, on écrit avec numpy
# des expressions qui impliquent des tableaux
# exactement comme si c'était des nombres
Z = np.cos(X)**2 + np.sin(X)**2 + 3

plt.plot(X, Z);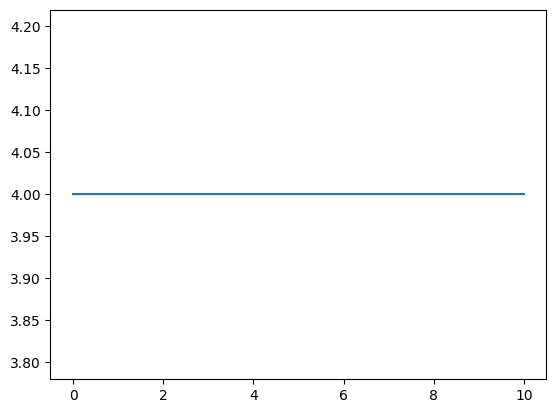

C’est le premier réflexe qu’il faut avoir avec les tableaux numpy : on a vu que les compréhensions et les expressions génératrices permettent de s’affranchir des boucles du genre :

out_data = []
for x in in_data:
    out_data.append(une_fonction(x))

on a vu en python natif qu’on ferait plutôt :

out_data = (une_fonction(x) for x in in_data)

Eh bien en fait, en numpy, on doit penser encore plus court :

out_data = une_fonction(in_data)

ou en tous les cas une expression qui fait intervenir in_data comme un tout, sans avoir besoin d’accéder à ses éléments.

ufunc¶

Le mécanisme général qui applique une fonction à un tableau est connu sous le terme de Universal function, ou ufunc, ça peut vous être utile avec les moteurs de recherche.

Voyez notamment la liste des fonctionnalités disponibles sous cette forme dans numpy.

Je vous signale également un utilitaire qui permet, sous forme de décorateur, de passer d’une fonction scalaire à une ufunc :

# le décorateur np.vectorize vous permet
# de facilement transformer une opération scalaire
# en opération vectorielle
# je choisis à dessein une fonction définie par morceaux
@np.vectorize
def scalar_function(x):
    return x**2 + 2*x + (1 if x <=0 else 10)

# je choisis de prendre beaucoup de points
# à cause de la discontinuité
X = np.linspace(-5, 5, 1000)
Y = scalar_function(X)
plt.plot(X, Y);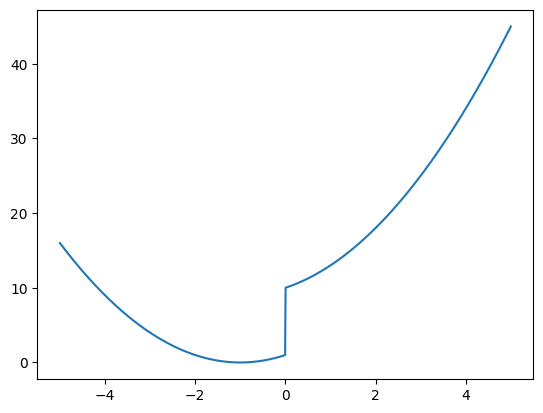

Conclusion¶

Pour conclure ce complément d’introduction, ce style de programmation - que je vais décider d’appeler programmation vectorielle de manière un peu impropre - est au cœur de numpy, et n’est bien entendu pas limitée aux tableaux de dimension 1, comme on va le voir dans la suite.