Complément - niveau basique¶
Ce support de cours reprend les notions de slicing vues dans la vidéo.
Nous allons illustrer les slices sur la chaîne suivante, rappelez-vous toutefois que ce mécanisme fonctionne avec toutes les séquences que l’on verra plus tard, comme les listes ou les tuples.
chaine = "abcdefghijklmnopqrstuvwxyz"
print(chaine)abcdefghijklmnopqrstuvwxyz
Slice sans pas¶
On a vu en cours qu’une slice permet de désigner toute une plage d’éléments d’une séquence. Ainsi on peut écrire :
chaine[2:6]'cdef'Conventions de début et fin¶
Les débutants ont parfois du mal avec les bornes. Il faut se souvenir que :
les indices commencent comme toujours à zéro ;
le premier indice
debutest inclus ;le second indice
finest exclu ;on obtient en tout
fin-debutitems dans le résultat.
Ainsi, ci-dessus, le résultat contient 6 - 2 = 4 éléments.
Pour vous aider à vous souvenir des conventions de début et de fin, souvenez-vous qu’on veut pouvoir facilement juxtaposer deux slices qui ont une borne commune.
C’est-à-dire qu’avec :
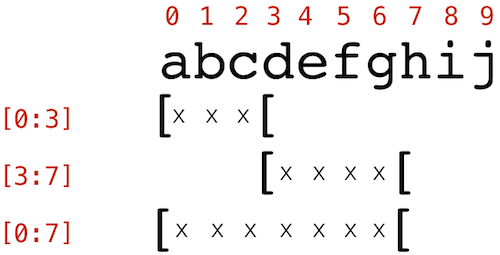
# chaine[a:b] + chaine[b:c] == chaine[a:c]
chaine[0:3] + chaine[3:7] == chaine[0:7]TrueBornes omises¶
On peut omettre une borne :
# si on omet la première borne, cela signifie que
# la slice commence au début de l'objet
chaine[:6]'abcdef'# et bien entendu c'est la même chose si on omet la deuxième borne
chaine[24:]'yz'# ou même omettre les deux bornes, auquel cas on
# fait une copie de l'objet - on y reviendra plus tard
chaine[:]'abcdefghijklmnopqrstuvwxyz'Indices négatifs¶
On peut utiliser des indices négatifs pour compter à partir de la fin :
chaine[3:-3]The history saving thread hit an unexpected error (OperationalError('attempt to write a readonly database')).History will not be written to the database.
'defghijklmnopqrstuvw'chaine[-3:]'xyz'Slice avec pas¶
Il est également possible de préciser un pas, de façon à ne choisir par exemple, dans la plage donnée, qu’un élément sur deux :
# le pas est précisé après un deuxième deux-points (:)
# ici on va choisir un caractère sur deux dans la plage [3:-3]
chaine[3:-3:2]'dfhjlnprtv'Comme on le devine, le troisième élément de la slice, ici 2, détermine le pas. On ne retient donc, dans la chaîne defghi... que d, puis f, et ainsi de suite.
On peut préciser du coup la borne de fin (ici -3) avec un peu de liberté, puisqu’ici on obtiendrait un résultat identique avec -4.
chaine[3:-4:2]'dfhjlnprtv'Pas négatif¶
Il est même possible de spécifier un pas négatif. Dans ce cas, de manière un peu contre-intuitive, il faut préciser un début (le premier indice de la slice) qui soit plus à droite que la fin (le second indice).
Pour prendre un exemple, comme l’élément d’indice -3, c’est-à-dire x, est plus à droite que l’élément d’indice 3, c’est-à-dire d, évidemment si on ne précisait pas le pas (qui revient à choisir un pas égal à 1), on obtiendrait une liste vide :
chaine[-3:3]''Si maintenant on précise un pas négatif, on obtient cette fois :
chaine[-3:3:-2]'xvtrpnljhf'Conclusion¶
À nouveau, souvenez-vous que tous ces mécanismes fonctionnent avec de nombreux autres types que les chaînes de caractères. En voici deux exemples qui anticipent tous les deux sur la suite, mais qui devraient illustrer les vastes possibilités qui sont offertes avec les slices.
Listes¶
Par exemple sur les listes :
liste = [1, 2, 4, 8, 16, 32]
liste[1, 2, 4, 8, 16, 32]liste[-1:1:-2][32, 8]Et même ceci, qui peut être déroutant. Nous reviendrons dessus.
liste[2:4] = [10, 20, 30]
liste[1, 2, 10, 20, 30, 16, 32]Voici une représentation imagée de ce qui se passe lorsqu’on exécute cette dernière ligne de code; cela revient en quelque sorte à remplacer la slice à gauche de l’affectation (ici liste[2:4]) par la liste à droite de l’affectation (ici [10, 20, 30] - ce qui a, en général, pour effet de modifier la longueur de la liste.
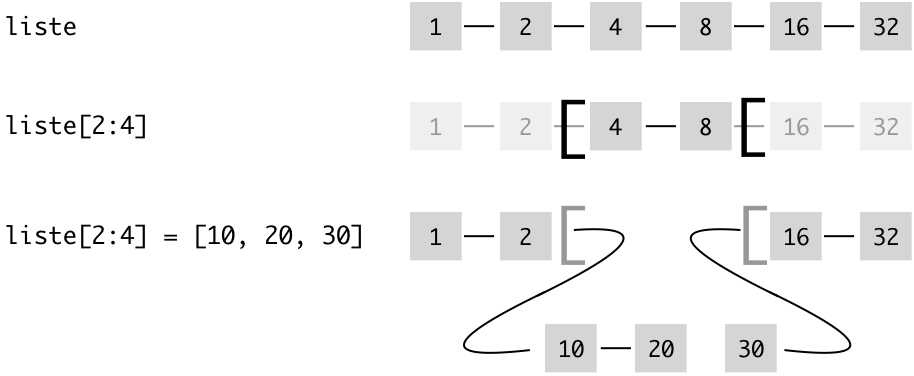
Complément - niveau avancé¶
numpy¶
La bibliothèque numpy permet de manipuler des tableaux ou des matrices. En anticipant (beaucoup) sur son usage que nous reverrons bien entendu en détail, voici un aperçu de ce que l’on peut faire avec des slices sur des objets numpy :
# ces deux premières cellules sont à admettre
# on construit un tableau ligne
import numpy as np
un_cinq = np.array([1, 2, 3, 4, 5])
un_cinqarray([1, 2, 3, 4, 5])# ces deux premières cellules sont à admettre
# on le combine avec lui-même - et en utilisant une slice un peu magique
# pour former un tableau carré 5x5
array = 10 * un_cinq[:, np.newaxis] + un_cinq
arrayarray([[11, 12, 13, 14, 15],
[21, 22, 23, 24, 25],
[31, 32, 33, 34, 35],
[41, 42, 43, 44, 45],
[51, 52, 53, 54, 55]])Sur ce tableau de taille 5x5, nous pouvons aussi faire du slicing et extraire le sous-tableau 3x3 au centre :
centre = array[1:4, 1:4]
centrearray([[22, 23, 24],
[32, 33, 34],
[42, 43, 44]])On peut bien sûr également utiliser un pas :
coins = array[::4, ::4]
coinsarray([[11, 15],
[51, 55]])Ou bien retourner complètement dans une direction :
tete_en_bas = array[::-1,:]
tete_en_basarray([[51, 52, 53, 54, 55],
[41, 42, 43, 44, 45],
[31, 32, 33, 34, 35],
[21, 22, 23, 24, 25],
[11, 12, 13, 14, 15]])