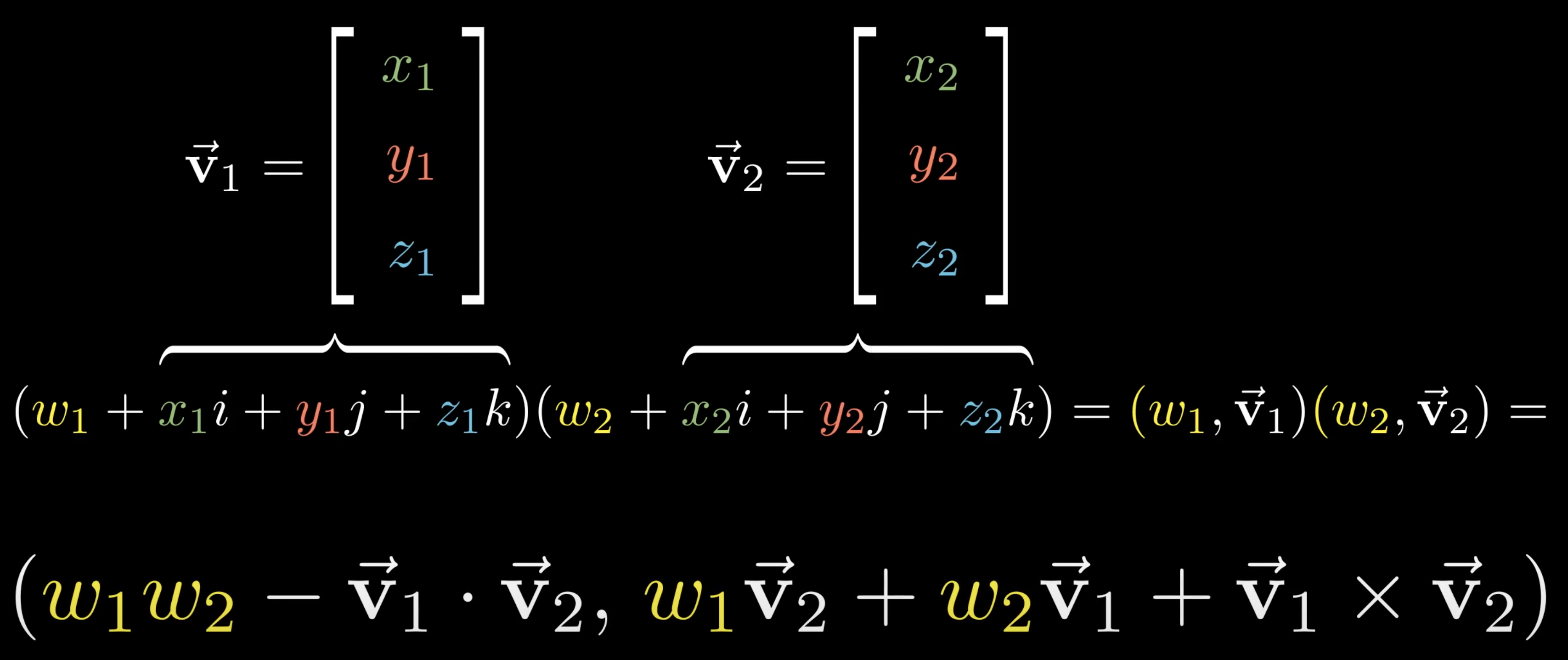Licence CC BY-NC-ND Thierry Parmentelat & Arnaud Legout Inria - UCA

exercice - niveau avancé¶

Le corps des quaternions est une extension non commutative du corps des complexes; la construction mathématique est totalement hors sujet pour nous, on va se contenter de ces quelques bribes :

les quaternions peuvent être vus comme un espace vectoriel sur $\mathbb{R}$ , un peu comme les complexes mais de dimension 4
un quaternion s’écrit donc $q = a + bi + cj + dk$
avec $(a, b, c, d) \in \mathbb{R}^4$
(les deux premiers éléments 1 et $i$ de cette base canonique sont ceux des nombres complexes)
les trois éléments $i, j, k$ sont tels que
$i^2 = j^2 = k^2 = ijk = -1$
(1)

attention : l’addition est bien commutative,
mais à nouveau la multiplication n’est pas commutative
ainsi par exemple $ij = k$ mais $ji = -k$

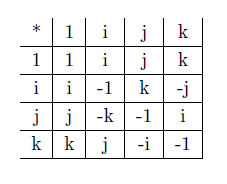
les règles indiquées ci-dessus impliquent (on vous laisse vous en assurer) que la table de multiplication est la suivante

On se propose ici d’écrire une classe pour représenter les quaternions.

Notes importantes

il est malheureux que Python ait retenu la notation j pour représenter ce qu’on appelle $i$ dans le corps des complexes, surtout dans ce contexte des quaternions où il y a un autre nombre qui s’appelle justement $j$ ...
le système de correction automatique a besoin également que votre classe définisse son comportement vis-à-vis de repr() ; regardez les exemples pour voir la représentation choisie, et inspirez-vous de la fonction number_str comme suit :

# vous vous souvenez des type hints ?
# sinon retournez voir la semaine 4 séquence 1

def number_str(x: float) -> str:
    """
    la fonction utilisée dans Quaternion.__repr__ 
    pour la mise en forme des nombres
    """
    if isinstance(x, int):
        return f"{x}"
    elif isinstance(x, float):
        return f"{x:.1f}"

from corrections.cls_quaternion import exo_quaternion
exo_quaternion.example()

# votre code

class Quaternion:
    
    def __init__(self, a, b, c, d):
        ...

# correction
exo_quaternion.correction(Quaternion)

# peut-être utile pour debugger ?
I = Quaternion(0, 1, 0, 0)
J = Quaternion(0, 0, 1, 0)
K = Quaternion(0, 0, 0, 1)

I*J == K

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Cell In[6], line 1
----> 1 I*J == K

TypeError: unsupported operand type(s) for *: 'Quaternion' and 'Quaternion'

J*K == I

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Cell In[7], line 1
----> 1 J*K == I

TypeError: unsupported operand type(s) for *: 'Quaternion' and 'Quaternion'

K*I == J

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Cell In[8], line 1
----> 1 K*I == J

TypeError: unsupported operand type(s) for *: 'Quaternion' and 'Quaternion'

I*I == J*J == K*K == -1

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Cell In[9], line 1
----> 1 I*I == J*J == K*K == -1

TypeError: unsupported operand type(s) for *: 'Quaternion' and 'Quaternion'

J*K == 1j

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Cell In[10], line 1
----> 1 J*K == 1j

TypeError: unsupported operand type(s) for *: 'Quaternion' and 'Quaternion'

K*J == -1j

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Cell In[11], line 1
----> 1 K*J == -1j

TypeError: unsupported operand type(s) for *: 'Quaternion' and 'Quaternion'

Quaternion(1, 2, 3, 4) == (1+2j) + J * Quaternion(3-4j)

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Cell In[12], line 1
----> 1 Quaternion(1, 2, 3, 4) == (1+2j) + J * Quaternion(3-4j)

TypeError: Quaternion.__init__() missing 3 required positional arguments: 'b', 'c', and 'd'

...

Ellipsis

comme exercice, vous pouvez aussi vous amuser à vérifier l’identité suivante (extraite de cette vidéo de 3blue1brown)